在现代科技迅速发展的今天，Web3作为一种新兴的互联网形态，影响着我们的生活和工作的各个方面。尤其是在区块链技术的基础上，Web3不仅仅是一个技术的革新，更是对人类社会互动和交易的根本性重塑。而在这个新的数字时代中，传统数学概念也迎来了新的机遇，圆周率作为一个重要的数学常数，同样在Web3中找到了它的应用之道。

圆周率的基本概念及其历史

圆周率是一个重要的数学常数，通常用希腊字母“π”表示。它表示圆的周长与直径的比值，是一个无限不循环的小数，数值约为3.14159。圆周率的历史可以追溯到几千年前的文明，古巴比伦和古埃及的数学家们就已开始对圆周率进行研究。随着数学的发展，圆周率的计算精度不断提高，计算机的出现使得π的计算达到了数十亿位甚至更多。

Web3对数学概念的需求与应用

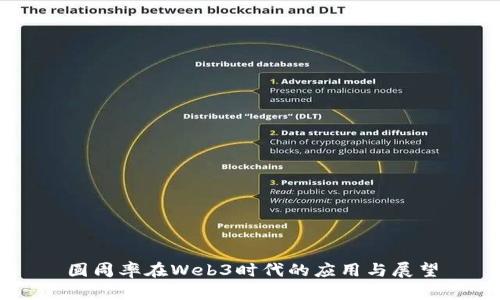
Web3强调去中心化、透明性和用户主控，这些特性使得许多传统的数学概念得到了重新审视。在数字资产、区块链应用、智能合约等领域，精确的计算能力和庞大的数据处理能力是必不可少的。这就为圆周率的应用提供了新的视角。在区块链加密技术中，很多加密算法的基础也涉及到复杂的数学计算，其中圆周率的应用不可忽视。

圆周率在区块链技术中的具体应用

圆周率在区块链的具体应用包括了但不限于加密货币算法、数据加密、算法交易、图形算法等方面。例如，许多加密货币如比特币和以太坊在其共识机制中，采用了数学上的复杂计算，涉及到递归和反馈算法等，这些计算在某种程度上需要准确的π值来保持精度。此外，智能合约在执行复杂财务计算时，往往也需要利用到圆周率进行可靠性验证。

当前Web3项目中圆周率的实际案例

在当前的Web3项目中，已经有一些团队开始探索圆周率在不同应用场景中的用途。例如，某些去中心化金融（DeFi）平台在计算利率时会用到相应的积分计算，而π作为一个重要的数学常数，能够有效地提高计算的精确度。此外，在NFT（非同质化代币）的创建与交易中，某些艺术作品通过特定算法生成，而这些算法也可能涉及圆周率的计算，从而形成独特的艺术风格。

圆周率在教育与推广中的角色

随着Web3的发展，对数学的关注度逐渐上升。对于教育者而言，如何用圆周率这样的数学概念在Web3中进行推广，是一个值得研究的方向。通过开发课堂项目、参与社区活动等方式，让更多的人了解数字资产和区块链的原理，以及如何利用圆周率进行实际应用的探索。

可能相关的问题探讨

Web3时代带来的数字转型，引发了许多用户和研究者的关注。以下是几个相关问题的探讨：

1. 圆周率在Web3中有哪些具体应用?

在Web3的众多应用中，圆周率的使用主要集中在数据加密和金融计算中。例如，在某些区块链技术中，利用圆周率进行复杂的加密运算，以确保交易的安全性。同时，在去中心化金融中，采用圆周率来计算利率累计、分红模拟等，也成为了一种颇具实际意义的尝试。此外，某些NFT项目也通过算法生成艺术作品，这些算法中涉及到的圆周率，可以赋予作品独特的数学美感，也从而吸引了大量用户的关注。

2. Web3中的数学算法如何影响金融交易?

Web3将传统金融与区块链技术结合，形成了新的金融交易模式。在这个过程中，数学算法被广泛应用于交易决策、风险评估等诸多环节。数学在此类应用中的重要性体现在两个方面：一是为交易提供科学的决策支持，另一方面则是通过算法降低报价的风险。例如，量力而行的算法会分析市场波动，利用圆周率等数学常数来做出更合理的交易选择，降低用户操作的风险。

3. 怎样更好地宣传圆周率在区块链中的应用?

为了更好地宣传圆周率在区块链中的应用，首先可以利用社交媒体和各种技术论坛对相关知识进行普及。其次，组织线上线下的研讨会，邀请行业专家分享关于数学与区块链的交叉领域。此外，开发互动性较强的教育软件，通过趣味活动和游戏，激发用户的兴趣，让更多的人了解圆周率在Web3时代的实际价值。

4. 如何看待圆周率的计算精度在未来技术中的作用?

随着计算技术的不断演进，圆周率的计算精度也在不断提升。未来，越来越多的应用场景需要高精度的数学常数，这不仅限于金融计算及加密技术。在量子计算、人工智能等前沿技术领域，圆周率的精度同样至关重要。因此，围绕如何提升计算能力的讨论将是未来技术发展的热点之一，相关的研究机构和企业也会对其加大投资力度，从而推动整个行业的发展。

5. 如何利用Web3技术促进数学教育的创新?

Web3技术的去中心化特性为数学教育带来了新的创新机会。通过区块链技术，可以创建开放的教育平台，教育者和学生能够在上面自由交流、共享知识。此外，利用智能合约，教育机构可以针对不同程度的学习者定制个性化课程，使其更加直观、高效。通过结合数学与技术的双重优势，可以吸引更多学生加入到数学学习中，进而提高整体的数学素养，培养未来科技发展所需的人才。

综上所述，圆周率在Web3时代正迎来新的机遇与挑战。通过不断深入探讨其在区块链及数字资产中的应用，相信能够为未来的科技发展提供源源不断的动力与支持。